相似度类型

在度量向量相似性时，相似度类型发挥着关键作用。选择恰当的相似度类型可以极大地提升分类与聚类的效果。

目前，Zilliz Cloud 支持以下相似度类型：欧氏距离（L2）、内积（IP）、余弦相似度（COSINE）、JACCARD 和 HAMMING**，**以及 BM25（适用于稀疏向量列的全文搜索）。

下表总结了不同字段类型与其对应的相似度类型的映射关系。

字段类型	维度范围	支持的相似度类型	默认相似度类型
FLOAT_VECTOR	2-32,768	COSINE, L2, IP	COSINE
FLOAT16_VECTOR	2-32,768	COSINE, L2, IP	COSINE
BFLOAT16_VECTOR	2-32,768	COSINE, L2, IP	COSINE
SPARSE_FLOAT_VECTOR	无需指定维度	IP, BM25（仅用于全文搜索）	IP
BINARY_VECTOR	8-32,768*8	HAMMING, JACCARD	HAMMING

📘说明

• 对于 BINARY_VECTOR 类型的向量字段，维度值（dim）必须为 8 的倍数。

下表展示了使用不同的相似度类型，其度量值的特点及取值范围。

相似度类型	特点	取值范围
L2	较小的 L2 距离表示更高的相似性。	[0, ∞)
IP	较大的 IP 距离表示更高的相似性。	[-1, 1]
COSINE	较大的 cosine 值表示更高的相似性。	[-1, 1]
JACCARD	较小的 Jaccard 距离表示更高的相似性。	[0, 1]
HAMMING	较小的 Hamming 距离表示更高的相似性。	[0, dim(vector)]
BM25	通过词频、逆文档频率、归一化文档长度评估相关性。	[0, ∞)

欧氏距离（L2）

欧氏距离主要是用来计算连接两点的线段的实际长度。

其计算公式如下：

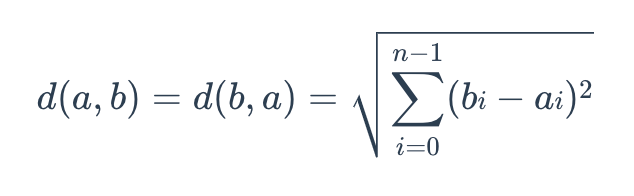
其中，a = (a₀, a₁,..., a_n-1) 和 b = (b₀, b₁,..., b_n-1) 表示 n 维欧氏空间中的两个点。

📘说明

在选择 L2 作为度量标准时，Zilliz Cloud 仅计算开方之前的数值。

内积（IP）

两个 Embedding 向量间的 IP 距离可按以下方式定义：

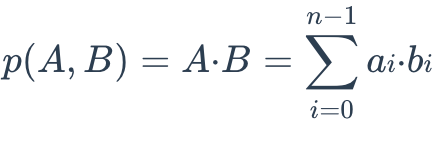
当处理未归一化的数据或关注数据的大小和方向时，内积尤为重要。

📘说明

使用 IP 计算 Embedding 向量间的相似度时，须先对 Embedding 向量进行归一化。之后，内积即可等同于余弦相似度。

例如，Embedding 向量 X 归一化为 X'：

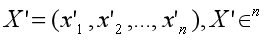
两个 Embedding 向量间的关联度如下所示：

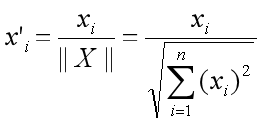
余弦相似度（COSINE）

余弦相似度是通过计算两组向量之间的夹角余弦来衡量它们的相似度。可以把这两组向量想象为从同一起点（如 [0,0,...]）出发，但朝向不同的线段。

计算两组向量 A = (a₀, a₁,..., a_n-1) 和 B = (b₀, b₁,..., b_n-1) 之间的余弦相似度，可使用以下公式：

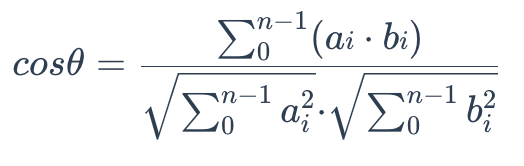
余弦相似度的值总是介于 [-1, 1] 之间。比如，两个向量的夹角越接近 0 度，余弦相似度越接近 1；两个向量的夹角为 90 度时，其相似度为 0；两个向量的夹角越接近 180 度，两个向量相似度越接近 -1。余弦值越大，表示两向量之间的夹角越小，意味着它们越相似。

通过 1 减去两向量间的余弦相似度，可以得到它们之间的余弦距离。

📘说明

该相似度类型目前还在测试阶段。升级您的集群至 Beta 版即可体验 COSINE 相似度类型。

JACCARD 距离

JACCARD 相似系数用于衡量两个样本集之间的相似度，其定义是两个集合交集的元素数量除以它们并集的元素数量。该系数仅适用于有限样本集。

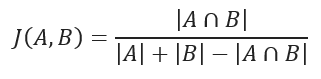
JACCARD 距离用于衡量数据集之间的不相似度，其计算方法是 1 减去 JACCARD 相似系数。对于二进制变量，JACCARD 距离等同于 Tanimoto 系数。

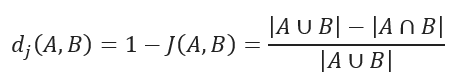
HAMMING 距离

HAMMING 距离用于测量二进制数据字符串。两个等长字符串之间的距离是它们在不同比特位上的数量。

例如，假设有两个字符串，1101 1001 和 1001 1101。 11011001 ⊕ 10011101 = 01000100。由于其中有两个 1，因此 HAMMING 距离 d (11011001, 10011101) = 2。